Strength and Geometric Sizes

of Pneumatically Spliced Combed

Wool Ring Spun Yarns

Stanisław Lewandowski,

Robert Drobina

University of Bielsko-Biała

Institute of Textile Engineering

and Polymer Materials

ul. Willowa 2, 43-300 Bielsko-Biała, Poland

Abstract

The strength and geometric sizes of wool combed yarns spliced under different conditions were investigated. The results indicated that only the time of preparing the yarn ends affects the strength of spliced yarns, whereas both the time of preparing the yarn ends and the splicing time affect the geometric size of these spliced yarns. The elongation at break of spliced yarns is very different from the analogous elongation of parent yarns, regardless of the splicer’s settings.

Key words: splicing strength, spliced yarns, elongation at break, dimensions.

n Introduction

In connection with the increasing demands made of yarn, the linking of the broken ends of yarn during winding by making weaver’s or fisherman’s knots has been almost completely replaced by the splicing linking of the yarn’s broken ends.

Because of the small dimensions of the cops, wound yarn from ring spinning frame contains about 40-60 junctions per yarn kg [1]. For example, during the weaving of shirt fabric, the loom elements encounter about 240 yarn places damaged by junctions of yarn per weaving hour. Apart from the places damaged by splicing, one should also take into consideration the yarn’s other faults.

In order to avoid these problems, some methods of ‘unknotted’ linking of the broken yarn ends have been developed. The most useful application has been the splicing technique, and the biggest success has been achieved by the use of the stationary devices named ‘splicers’ mounted on automatic winding machines.

The joints produced by pneumatic splicing should have no great mass variations, present no mechanical obstructions, and have almost equal elasticity with the original yarn under both static and dynamic loading. The external view and physical properties of the spliced yarns should be similar to the external view and physical properties of the rest of the yarns, but achieving an ‘ideal joint’ is impossible. The splices also should contain no extraneous material, so that the dye affinity should remain unchanged at the joint. Fulfilling of these demands will provide a wider possible application range considering the kind of the fibres used, as well as the yarn counts [4-6]. A correct splicing of the fibre ends broken depends among others on their preparing.

In modern textile mills, control of the technological process is carried out through the USTER control apparatus made by Zellweger [7]. This company produces the modular, microprocessor-controlled yarn cleaning device [7]. The apparatus continuously monitors thick and thin places, neps and yarn count faults, and ‘splices’ in six independent, practice-oriented channels. Alarm functions allow a shut-down of the machine’s winding positions if yarn of unsuitable quality is manufactured. The cut forecast through ‘virtual clearing’, which counts but does not extract yarn faults, facilitates the optimisation of the clearing parameter settings over winding. It may be assumed that in foreseeing future Zellweger will complete the Uster Statistics extended by ‘virtual’ yarn faults derived from ‘virtual cleaning’.

The great majority of investigations concerning ‘unknotting linkages’ has been focused on the physical properties and view of spliced yarns. Bissman [8], Gebald [9], Kaushik, Sharma, Hari [10-13], and Frontczak-Wasiak & Snycerski in Poland [14] have performed such investigations.

No publication has been found about the optimisation of the splicing devices. Not before 2000, as Cheng and Lam [15] [16] from South Korea have undertaken the first attempt in this field. These authors determined the relationship between the settings of the Mesdan Jointair 114 pneumatic splicer, supplemented with nominal physical yarn properties (linear mass - tex, twist factor) and the physical properties of spliced yarns manufactured from cotton/polyester 65/35 blended ring-spun yarns [15] and cotton ring-spun yarns [16].

For blended yarns, the authors tested and analysed only the strength of pneumatically spliced joints. In the case of cotton yarns, besides strength the authors determined bending rigidity and abrasion resistance. They also organoleptically assessed the appearance of the spliced yarns. The results fall into five linguistically determined grades as follows:

1 = failure or totally unacceptable,

2 = marginally acceptable,

3 = acceptable,

4 = good, and

5 = ideal (not different from non-spliced yarn) [16].

In order to build statistical models, the authors [15,16] used orthogonal analysis and linear regression.

The investigations related to the optimisation of the splicer device were performed in Poland on the example of jointing post-breakage threads manufactured from combed-wool ring-spun yarns. These tests have been conducted since 1988 and continue to the present day in the Institute of Textile Engineering and Polymer Materials (University of Bielsko-Biała), in co-operation with the Weldoro spinning mill. The preliminary results of the tests were published in articles [2,3]. In this paper, we present results derived from the years 2000-2003 [18-21] concerned with the optimisation of the splicer device on the example of jointing after breakage of 25-tex wool-combed ring-spun yarn.

n Experimental

Wool-combed ring-spun single yarns (Table 1) were used for the experiment. Single cops were manufactured on the Fiomax 20000 ring-spinning machine from Suessen. A Mesdan Jointair 4941 pneumatic splicing device [22] installed on the Espero winding machine [23] produced all the spliced yarn joints.

Experimental scheme construction

The Mesdan Jointair 4941 device has four regulation points for adjusting the splicing conditions [22]:

§ time of splicing cycle t_A, (0, 1, 2, 3, 4, 5) (dimensionless settings)

§ length of the yarn ends not spliced in the joint l_B, (0, 1, 2, 3, 4, 5, 6, 7, 8) (dimensionless settings),

§ air volume during splicing cycle V_C (stepless adjustment) (litre/per

1 splice),

§ time of preparing yarn ends for splicing t_E (0, 1, 2, 3, 4, 5) (dimensionless settings).

Studying the preliminary tests, we can assume the values l_B and V_C as constant, because it is already possible to organoleptically assess the properly splicing yarns joints during the working of the splice device. Investigations in optimising the process of splicing yarn ends were designed on the basis of the function of two variables t_A and t_E, because we acknowledged that making alterations to the specified input variable only makes sense when they are taken into account in connection with the other input variables [17].

We designed the total experiment [24], of the 5×5 type, according to Figure 1. As the constant values recommended by the Mesdan company, we accepted l_B=4 and V_C=0.6 litre per splice).

Test conditions methodology

Strength parameters

The Instron 5544 tensile tester was used to test the breaking strength properties of all the original and spliced yarns. The specimen length was set to 500 mm, and as a result both the parented yarns and the spliced yarns were determined from 50 ends/per variant. Specimens were mounted in the clamps in such a way that the spliced linkage of the yarn was in the middle of the clamp distance in the tensile tester. While performing the tests we took into account only these measurements in which the breaking of spliced yarn was situated exactly at the place of jointing.

We determined the following quantities:

§ breaking forces of parent and spliced yarns - Fr_n; Fr_p [cN],

§ elongation at break of parent and spliced yarns - Er_n; Er_p [%],

§ breaking tenacity of parent and spliced yarns - Wt_n; Wt_p [cN/tex].

In order to observe the differences between the strength properties of the parent and the spliced yarns, we determined the following quantities:

§ coefficient of strength retention of the joint η_W=Wt_p/Wt_n.100 [%]. Cheng and Lam [15,16] determined it as the strength of the spliced yarn expressed as the percentage of the parent yarn in which the splice was inserted, and they defined it as retained spliced strength - RSS;

§ coefficient of elongation at break retention of the joint η_E=Er_p/Er_n.100.

These coefficients were taken into account while computing the statistical data analysis.

Geometric sizes

In order to determine the geometric sizes of the spliced joint yarns, we performed an image analysis of the yarn joints with the help of a measuring work-stand, composed of a Panasonic Nikon-800 video camera and a Steddy-T type stereoscope microscopefrom Ceti and a computer. The view of spliced joints which was registered on the monitor was subjected to digital image analysis with the help of Microscan 1.3 software. In order to achieve better differentiation of both the brightness and colour of the observed yarn specimens, we used an high-pass Laplace filter to emphasise differences between the brightness and colour of adjacent pixels [25,26]. Three kinds of Laplace filter exist, differentiated by filter mask and therefore by the degree of filtration. We were able to choose the kind of filter mask F₁, F₂ and F₃ on the basis of the automatic command ‘Laplace Transform’; the matrixes of these filters had the following form:

(1)

On the basis of the appearance of the image-spliced joints, we determined (according to Figures 2 and 3):

§ the lengths of the yarn spliced joints l_p,

§ the transversal dimensions of the parent yarns d_n [mm],

§ the transversal dimensions of the spliced yarns d_p [mm], and

§ the length of the joint ends, not spliced to linkage l_k [mm].

We performed 50 measurements for each variant.

A detailed methodology of the determination of the geometric sizes was presented in articles [2,3]. In order to observe the differences between geometric sizes of the parent and the spliced yarns, we determined the coefficient of the increase in the transversal dimension λ_D [%]:

(2)

Methods of data analysis

Textile processes belong to the class of stochastic processes, in which the object output is a function of the inputs x₁, x_2, x₃, ... , x_s and non-measurable disturbances - z. One may classify the process of jointing yarns after breakage by the pneumatic splicing technology as a stochastic process.

In order to assess the results of the technological settings operating in the splicing device, we applied the F-Snedecor test of variance analysis according to double classification [27], and then we performed the statistical description of the adopted model of an investigated object with the help of regression functions approximated by linear and square multinomials with the form:

Y₁ = B₀ + B₁ . t_E + B₂ . t_A +

+ B₁₁ . t_E² + B₂₂ .t_A² + B₁₂ .t_E .t_A, (3)

and

Y₂ = B₀ + B₁ . t_E + B₂ . t_A +

+ B₁₁ . t_E² + B₂₂ .t_A² + B₁₂ .t_E .t_A, (4)

where:

B₀ ; B₁ ; B₂ ; B₁₁ ; B₂₂ ; B₁₂ - the coefficients of the regression function.

We determined the unknown values of the coefficients of regression function based on the minimisation deviation of the sum square, using the following formula [24]:

, (5)

where:

B - the coefficients of regression function vector,

X - the experimental matrix,

X^T - the transposed matrix,

Y - the output vector of the object,

(X^T X)^-1 - the reverse (covariance) matrix.

We assessed the consistency between the model output and the object output on the basis of the value of the coefficient of determination R, using the following formula [24]:

, (6)

where:

y_n - the object output in the n-test,

y_n - the model output in the n-test,

N - the number of tests in the experiment, and

y - the mean value of the object output and the model output.

Assessing the relationship between the splicing device settings and strength properties and geometric sizes, we also analysed (besides the multidimensional determination coefficient) the analytical values of the F-Snedecor statistics

F (K; N - K - 1) which assessed the sig-nificance of the computed regression function by the formula:

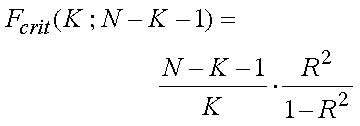, (7)

where:

F_crit - the critical values of the F-Snedecor statistics determined for K and N - K - 1 degrees of freedom at the significance level α=0.05.

t_crit ( N - K - 1) - the critical values of the t-Student statistics determined for N - K - 1 degrees of freedom at the significance level α=0.05.

n Results and Discussions

Analysis of the strength parameters of spliced yarns

The results of the experiment and the statistical computations are shown in Tables 2, 3 and 4 respectively. According to Table 2, the particular strength properties of spliced yarns are changed within the following boundaries:

§ breaking force from 101.38 cN (E3A5) to 139.59 (E1A4),

§ relative elongation at break from 4.01% (E3A5) to 7.0% (E1A2),

§ breaking tenacity from 4.03 cN/tex (E0A2) to 5.58 cN/tex (E1A4),

§ coefficient of strength retention of the joint from 66.70% (E3A5) to 91.84% (E1A4),

§ coefficient of elongation at break retention of the joint from 41.01% (E3A5) to 71.53% (E1A2).

Analysing the data in Table 3, we can state that only the time of preparing yarn ends to splicing t_E affects the strength properties of spliced yarns, whereas the time of splicing cycle t_A does not significantly influence these properties.

Analysing the data in Table 4, we can state that neither the function η_W= f(t_E;t_A) nor η_E=f(t_E;t_A) are suitable for mathematical presentation (significance level α=0.05) with the help of linear and square multinomials, because the coefficient of determination values are very small - R<0.3. Furthermore, the computed values of the

F-Snedecor statistics are smaller than their critical values; therefore these functions are not significant.

Because the time of the splicing cycle t_A has no significant influence on the values of the analysed coefficients in this connection, we attempted to establish the relationships η_W = f(t_E) and η_E = f(t_E). We have approximated these functions with the help of a third-degree multinomial (Figures 4 and 5).

In spite of the very high values of the multidimensional determination coefficients, the regression functions as determined were not statistically significant. Regardless of the splicing cycle t_A, the most favourable spliced yarn joints in respect of its coefficient of strength retention and coefficient of elongation at break retention may be achieved when the time of preparing yarn ends to splicing t_E=1.

This phenomenon can be explained as follows. While performing pneumatically spliced joints from wool-combed ring-spun yarns with a normal twist of Z630, it is not necessary to apply long t_E periods in order to obtain the effect of untwisting of the yarn ends prepared. Its increase causes an entangling of fibres in the splicing chamber, and in extreme cases, an over-twisting of fibres in the air stream. It disadvantageously influences the splicing phase and causes a decrease in the values of parameter η_W and η_E over a longer time t_E.

Analysis of the geometric sizes of spliced yarns

The results of the experiment and statistical computations are shown in Tables 5, 6 and 7 respectively. According to Table 5, the particular geometric sizes of spliced yarns are changed within the following boundaries:

§ the length of joint l_p from 12.6 mm (E0A1) to 23.8 mm (E4A5),

§ the length of joint ends, not spliced to linkage l_k from 2.9 mm (E3A5) to 9.95 mm (E0A5),

§ the coefficient of increase in the transversal dimension λ_D from 42.76% (E4A3) to 73.55% (E0A5).

Analysing the data in Table 6, we can state that the alteration of the splicer’s settings t_E and t_A influences the individual (particular) geometric sizes of spliced yarns as follows:

§ the length of joint l_p: (t_E - yes, t_A - yes),

§ the length of joint ends, not spliced to linkage l_k: (t_E - yes, t_A - no),

§ the coefficient of increase in the transversal dimension λ_D: (t_E - no, t_A - no).

Analysing the data in Table 7, we can state that the regression functions

η_W= f(t_E;t_A) and η_E=f(t_E;t_A), as approximated with the help of a linear-square multinomial, are statistically significant. Graphic images of the acting times t_E and t_A for the individual geometric sizes of spliced yarns are shown in Figures 6, 7 and 8.

Both analysed settings of the splicing device influence the length of the spliced joint, but the impact of the time t_A is greater than the action of the time t_E. We observed a more intensive increase in the length of spliced yarn within the range of small value times, both t_A and t_E.

Together with the increase in time t_A, throughout the whole analysed range of time t_E, the length l_p increases up to the value determined by formula

t_A = 4.005 - 0.0932 . t_E,

and after exceeding this value, the length l_p decreases. The analysed regression function has no local extreme.

Both the analysed parameters t_E and t_A (to almost the same degree) on the length l_k of joints’ ends, not spliced to linkage (Figure 7). Together with the increase in times t_E and t_A, the length l_k decreases.

Both the analysed parameters t_E and t_A impact (to almost the same degree) on the increase in the transversal dimension λ_D (Figure 8). This influence is very complex and diversified in the individual sub-ranges in both times analysed.

When the values of splicing time t_A are not as large, regardless of the time t_E of preparing yarn ends to splicing, one can observe only insignificant changes in the parameter λ_D. But in the range t_A=3-5 and t_E=0-3, together with the simultaneously decreasing t_A and increasing t_E, the coefficient λ_D of the transversal dimensions of spliced yarns decreases. The analysed function has no local extreme.

n Conclusions

§ The generalised properties of pneumatic spliced yarns (strength parameters and geometric sizes), are more influenced by changes in t_E and less intensive by changes in t_A.

§ The variability of the considered strength parameters and geometric sizes of pneumatic spliced yarns caused by simultaneously changing both parameters t_E, t_A in respect of power interaction proceeds as follows: λ_D > l_p > l_k > η_W > η_E.

§ The coefficient of strength retention of the joint runs within the boundaries η_W=66-92%, and so it is possible to select such settings of the Jointair 4941 splicer whereby the breaking strength of spliced yarn is almost the same as the strength of the parent yarn.

§ It is regrettable that the coefficient of elongation at break retention of the joint runs within the boundaries η_E=41-71%, because regardless of the applied splicer settings, the breaking elongation of spliced yarn is very distinct from the analogous elongation of the parent yarn.

§ In order to better identify the jointing process by pneumatic splicing yarns, it is necessary to continue investigations into the following questions:

§ the fatigue strength properties of splicing joints,

§ the organoleptic and expert assessment of non-measurable features of splicing joints,

§ image analysis of the splicing joint with the help of statistical and morphological approaches, and

§ the analysis of appearance & image and the physical properties of splicing joints with the help of artificial intelligence elements.

References

1. Artzt P. Perspektiven des Ringspinnverfahrens, Institut für Textil- und Verfahrens- technik der DITF Stuttgart, Denkendorf. Melliand Textilberichte, 79 (1998), p. 125.

2. Machnio M., Drobina R.: Assessment of physical properties pneumatically spliced wool combed ring spoon yarns, Przegląd Włókienniczy & Technik włókienniczy 54 (10/2000), pp. 3-7.

3. Machnio M., Drobina R.: Visual assessment of pneumatically spliced ends joints manufactured from wool combed ring spun yarns, Przegląd Włókienniczy & Technik włókienniczy 55 (01/2001), pp. 12-14.

4. Cheng K.P.S., Chan, K.K., How Y.L. and Lam H. L. I., Spliced Yarn Qualities - Breaking Strength and Flexural Rigidity of Spliced Yarns, Textile Asia (5), 45-47 (1997).

5. Kaushik R.C.D., Sharma, I.C. and Hari P.K., Effect of Fibre/Yarn Variables on Mechanical Properties of Spliced Yarn, Textile Research Journal, 57 (08/1987), pp. 490-494.

6. Lam H.L.I. and Cheng K.P.S., Pneumatic Splicing, Textile Asia (7), 66-69 (1997).

7. Survey of products - PE 4051 - Uster-Zellweger prospectus, 1997.

8. Bissman O., Herstellung Knotfreier Garnverbindungen durch das Splice-Verfahren. ITS, 3 (1981).

9. Gebald G., Splicing technology in auto-winding. Textile Month, 7 (1982).

10. Kaushik R.C.D., Sharma I.C., Hari, P.K., Mechanism of Splice, Textile Research Journal 58 (05/1989), pp. 263-268.

11. Kaushik, R.C.D., Sharma I. C., Hari P.K. Quantitative Contribution of Splice Elements, Textile Research Journal, 58 (06/1989), pp. 343-345.

12. Kaushik, R.C.D., Sharma, I.C., Hari, P.K., Effect of Fibre/Yarn Variables on Mechanical Properties of Spliced Yarn, Textile Research Journal, 57 (08/1987), pp. 490-494.

13. Kaushik R.C.D., Hari P.K., Performance of spliced yarn in warping and weaving. Textile Research Journal, 57 (1987), 670.

14. Frontczak-Wasiak I., Snycerski M., Criteria of assessment of spliced yarns, Przegląd Włókienniczy & Technik Włókienniczy, 46 (01/1992), pp. 7-10, Przegląd Włókienniczy & Technik Włókienniczy, 46 (02/1992 r), pp. 33-35.

15. Cheng K.P.S., Lam H.L ., Strength of Pneumatic Spliced Polyester/Cotton Ring Spun Yarns, Textile Research Journal, 70 (03/2000), pp. 243-246.

16. Cheng K.P.S., Lam H.L ., Physical Properties of Pneumatically Spliced Cotton Ring Spun Yarns, Textile Research Journal, 70 (12/2000), pp. 1053-1057.

17. Masters T., Artificial neural networks in practical usage, WNT Warszawa 1996.

18. Lewandowski S., Drobina R., Cebrat J., Assessment of Jointair device settings spliced yarns ends, Research report. University of Bielsko-Biała, 2002.

19. Machnio M., Drobina R., Zuśka T., Assessment of strength parameters of pneumatically spliced yarns ends after breakage, Research report. Akademia Techniczno-Humanistyczna, Bielsko-Biała, 2003.

20. Lewandowski S., Drobina R., Walentek M., Optimisation of splicing device with the aspect of joint appearance, Research report. University of Bielsko-Biała, 2003.

21. Lewandowski S., Stańczyk T., Classification of spliced yarns joints using artificial neural networks, Research report. University of Bielsko-Biała, 2003.

22. Servicing instruction of Espero automatic winder, Savio Company.

23. Servicing instruction of Jointair 4941 splicer, Mesdan Company.

24. Mańczak K., Methods of identification of multidimensional objects control, WNT, Warsaw, 1979.

25. Servicing instruction of Microscan Software 1.3.

26. The Great Informatic and Computer English-Polish Dictionary, Publishing House Electronics ISBN 83-86192-13-4, 1^st edition.

27. Greń J. Mathematical statistics models and