Approximate Study on a Tensile Model of Wool/spandex Core-spun Yarn
Min Dang,
Shanyuan Wang
College of Textiles,
Dong Hua University,
Shanghai, 200051, People’s Republic of China
E-mail: mindang99@mail.dhu.edu.cn
Abstract
An approximate approach is presented to calculate and predict the specific stress of wool/spandex core-spun yarn, based on an idealised yarn structure model and Hearle’s yarn theory. The approximate model covers some major parameters from wool fiber, spandex and core-spun yarn. Comparing with experimental tensile (stress-strain) curves of core-spun yarn, we can see that the theoretical model can basically reflect the shape of wool/spandex core-spun yarn’s tensile curve and the model is useful for predicting the stress-strain behaviour of wool/spandex core-spun yarn at small extension.
Key words: core-spun yarn, spandex, specific stress, stress-strain curve, tensile strength.
List of symbols
D - the drafting ratio of spandex during spinning
Ef - wool fibre modulus
Esp - spandex modulus
F - force of the whole core-spun yarn
- stress in corresponding outer layer in continuous filament yarn (radius vary from rs to R)
- stress in outer wool fibre layer in core-spun yarn (radius vary from rs to R)
Fsp - force of spandex with elongation (D - 1) × 100% + εy
G - specific stress, perpendicular to fibre axis
Lf - wool fibre length
Nsp.tex - linear density (tex) of spandex
r - radius position of fibre in yarn
R - core-spun yarn radius
rf - wool fibre radius
rs - spandex radius
Q - wool fibre migration period
X - tensile specific stress of wool fibre in yarn
α - yarn surface helical angle
β - stress reduction coefficient in staple fibre yarn compared with that of continuous filament yarn
εf - wool fibre strain
- the mean wool fibre strain
εy - axial strain in yarn
γ - correcting factor to modify the retraction of spandex between front nip and traveller during spinning
µ - coefficient of friction between wool fibre
νy - specific volume of core-spun yarn
σ - specific stress of core-spun yarn
σ1 - axial Poisson’s ratio of wool fibre
σy - axial Poisson’s ratio of core-spun yarn
n Introduction
The properties of yarn play a vitally important part in affecting the properties of fabrics and downstream processing. The recently emerged new spinning methods, such as Sirospun, Sirofil, Solospun and the Compact spinning technique, have opened new fields for the analysis of the mechanical behaviour of yarn.
The difficulties in analysing the mechanics of staple yarns lie primarily in three factors [1 - 5]. The first is the discontinuities in fibre length that consequently cause partial slippage during yarn extension. To solve the problem, Gregory [1] derived a formula relating the critical length to fibre character parameters and pressure between fibres. Ning Pan [3] took the coherence brought into play by lateral pressures between fibres as a key factor to determine slipping or not. Another difficulty comes from twist [6 - 8]. The complex relation between twist and friction has been studied by researchers in this area [5, 9 - 11]. The last difficulty concerns yarn structure, which involves the radical position of fibre in yarn and disuniformity of yarn specific volume.
Theoretical tensile model of core-spun yarn
Wool/spandex core-spun yarn is subdivided into two parts, as shown in Figure 1, the inner part is spandex with radius rs, the wool fibres cover spandex as the outer part and the whole yarn’s radius is R. We would study the mechanics of sheath and core, respectively. The analysis of the outer layer can be carried out according to staple yarn theory. The tensile stress of the whole core-spun yarn is the sum of stress that ??? in the two parts. Yarn structure meets the requirements of a perfect helical model. All wool fibres are assumed to have identical properties. The yarn has a uniform specific volume. There is assumed to be a uniform distribution of stress across each face of a yarn element. The shear forces acting on the faces of the element are neglected. Spandex is assumed to be perfectly elastic.
Assuming the same stress reduction in each layer, Hearle [2] proposed a parameter 
β as stress reduction in staple fibre yarn compared with that of continuous filament yarn. Using the assumption above, stress in the outer wool fibre layer in core-spun yarn can be expressed as:
β =
/
(1)
where:
- is the stress in the outer wool fibre layer in core-spun yarn (layer radius vary from rs to R),
- in the stress in the corresponding outer layer in continuous filament yarn (layer radius vary from rs to R) Equation 1 can be rewritten as
= β
(2)
The steps to calculate stress in the outer layer of core-spun yarn are as follows.
1st step. Write down the components, parallel to yarn axis, of forces across the section of the yarn lying between radius r and (r + dr) in Hearle’s filament yarn theory.
(3)
where:
R - yarn radius,
νy - specific volume of yarn,
c = cos α,
α - yarn surface helical angle,
r - radius position of fibre in yarn, X - tensile specific stress of fibres in yarn, G - specific stress, perpendicular to fibre axis.
The formula of X and G is given by Hearle [4]. In Hearle’s work, specific stress is defined as the ratio of the force to the mass/unit length. It is a more convenient quantity than the conventional stress (force/unit area) for textile applications. So this notion is still adopted here.
2nd step. Integrate above force component with radius varying from rs to R to get
.
When radius varies from rs to R, parameter u varies from 
to 1, for convenience, denote 
, then we have
equation (4).
Combining Equation 4 with formula of X and G, and using the procedure shown in Appendix, we can get the solution of the integral Equation 4 in the form of Equation 5.
3rd step. Write down the formula of parameter β given by Hearle and calculate
according to Equation 2.
(6)
Then the force acting on the outer layer in core-spun yarn is determined by Equation 7, were:
Q - migration period,
Lf - fibre length,
µ - coefficient of friction,
rf - fibre radius,
σ1 - axial Poisson’s ratio of fibre,
σy - axial Poisson’s ratio of yarn.
Xf = Efεy, εy - axial strain in yarn,
Ef - fibre modulus.
Denote parameter D as the drafting ratio of spandex during spinning. Spandex modulus Esp can be obtained from its tensile curves. Nsp.tex - linear density (tex) of spandex yarn, γ is the correcting factor to modify the retraction of spandex between front nip and traveller during spinning. It is an empirical value. So the force of spandex with elongation (D - 1) × 100% + εy is
Fsp = Esp.Nsp.texγ[(D - 1)×100%+εy] (8)
From Equation 7 and 8, we have the force of the whole core-spun yarn as F presented by Equation 9.
+
+ Esp . Nsp.texγ[(D - 1) × 100% + εy] (9)
According to the definition of specific stress σ by Hearle (σ = Fνy/S, S is the acting area of force F, we obtained the specific stress σ in the whole core-spun yarnin the form of equation 10.
In Equation 10, fibre modulus Ef varies with slope of the point at tensile curve. Ning Pan derived a formula to connect the mean fibre strain
and yarn strain as Equation 11.
(11)
Then substituting
for εf, ε can be obtained. Tensile curves of core-spun yarn then can be got from Equation 10 and wool fibre stress-strain curves.
n Evaluation of the analysis
To evaluate the accuracy of the analysis presented above, three types of core-spun yarn were produced on modified worsted spinning frame. We used 70D Lycra® produced by DuPont as the yarn core. Fibre and yarn parameters used in experiments are listed in Tables 1 and 2. The fibre tensile curve is shown as Figure 2. The Theoretical and experimental tensile curves of core-spun yarn are shown in Figures 2 - 4. The measurements of all parameters are according to China National Standard for Textiles. The experimental tensile curve of core-spun yarn is obtained as the mean value of that of 50 yarn tensile curves. And the experimental tensile curve of wool fibre is the mean value of that of 250 wool fibre tensile curves. Note that yarn No. 3 has such a high twist that it breaks at about 9% elongation.
From Figures 2 - 4, it can be seen that the theoretical and experimental curves possess similar shape and meet at a certain point of low yarn extension, i.e. the predicted theoretical value is larger than its real value at low yarn extension and smaller than the real value at high yarn extension. The conformability effect of yarn No. 3 is much better than others.
The reason that yarn No. 3 has a better conformability effect can be explained as follows: the twist of yarn No. 3 is comparatively high and yarn configuration is similar to that of continuous filament yarn. During yarn extension, slippage in yarn is difficult to occur as obviously and fluently as in low twist staple yarn. So parameter β is closer to the real value, which directly leads to a better conformability effect.
At large yarn extension, the fibre slippage length increases monotonously when fibre position varies from the centre of to the surface of yarn [1]. And slippage length on the yarn surface is much larger than that at the yarn’s core. So parameter β at the yarn surface position would in turn be much smaller than that at the yarn’s core. In this paper, the assumption that all the layers have the same stress reduction as the surface layer would doubtless cause smaller yarn stress than that of experimental yarn. However the decrement of parameter β on the yarn surface and at the yarn’s core will be not so obvious during low yarn extension. So the difference is mainly caused by the greater value of the empirical parameter γ, which then leads to a more obvious diff-erence when εy = 0. The difference will be compensated and in turn decreased by the decreasing component caused by the error of parameter β.
Another interesting phenomenon can be seen from Figures 2 - 4. Both theoretical and experimental curves do not start from origin, which means that stress in yarn is not equal to zero even when there is no extension of the yarn. When εy = 0, then
= 0. But Fsp ≠ 0. Fsp
is generated by spandex drafting during spinning. During testing of yarn tensile properties, a pre-tension should be set to make yarn straight but not extended. A universal standard of the pre-tension is 1 cN/tex. So the yarn stress is not equal to zero when εy = 0.
n Conclusion
In this paper, a new approximate app-roach is presented to calculate and predict the specific stress of wool/spandex core-spun yarn, based on an idealised structure model and Hearle’s yarn theory. The resulting equation of specific stress of wool/spandex core-spun yarn includes some major parameters: parameters of wool fibre (radius, length, specific density, modulus, Poisson’s ratio and frictional coefficient), parameters of spandex yarn (radius, modulus and drafting ratio) and parameters of core-spun yarn (migration period, count, twist and Poisson’s ratio). By verifying with experimental tensile curves of core-spun yarn, we can see that the theoretical model is valid in predicting the tensile behaviour of wool/spandex core-spun yarn and the model is useful for predicting the stress-strain behaviour of wool/spandex core-spun yarn at small extension.
References
1. Gregory J.; J Text Inst, 44 (1953) T499.
2. Hearle J. W. S.; Text Res J, Vol. 35 (1965) p. 1060.
3. Pan Ning; Text Res J, Vol. 63 (1993) p. 504.
4. Hearle J W S, J Text Inst, Vol. 49 (1958) p. 389.
5. Postle L. J., Ingham J.; J Text Inst, Vol. 43 (1952) T77.
6. Pan Ning; Text Res J, Vol. 62 (1992) p. 749.
7. Grosberg P., Smith P. A.; J Text Inst, Vol. 57(1966) T15.
8. Carnaby G. A., Grosberg P.; J Text Inst, Vol. 67 (1976) p. 299.
9. Lincoln B.; J Text Inst, Vol. 45 (1954) T92.
10. Viswanathan A.; J Text Inst, Vol. 57 (1966) T30.
11. Campos R., Bechtold T., Rohrer C.; Text Res J, Vol. 73 (2003) p. 721.
Figure 1. Cross-section of wool/spandex core-spun yarn.
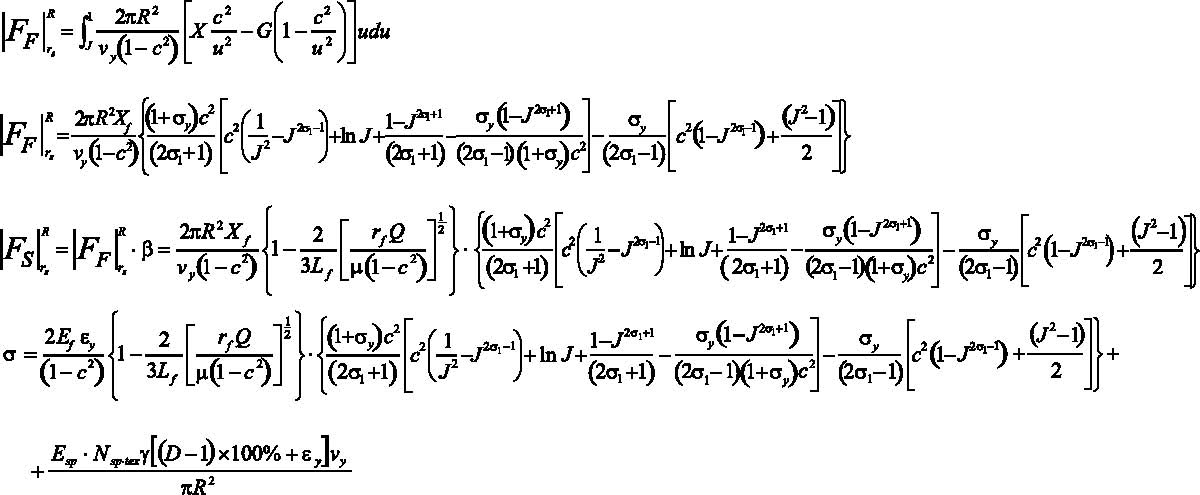
(4)
(5)
(7)
(10)
Equations: 4, 5, 7, and 10.
Table 1. Some parameters of wool/spandex core-spun yarn.
|
No. of yarn |
Linear density of yarn/tex |
Twist of yarn, t.p.m. |
|
1 |
29.42 |
480 |
|
2 |
30.26 |
630 |
|
3 |
32.66 |
850 |
Table 2. Fiber parameters.
|
Parameter |
Value |
|
Wool fiber |
|
|
Fiber radius, cm |
1×10-3 |
|
Fiber length, cm |
8 |
|
Fiber specific density, g/cm3 |
1.2 |
|
Fiber coefficient of friction |
0.25 |
|
Poisson’s ratio of fiber |
0.8 |
|
Spandex |
|
|
Fiber radius, cm |
4.523×10-3 |
|
Fiber modulus, cN/tex |
1.1 |
|
γ |
0.862 |
|
D |
3 |
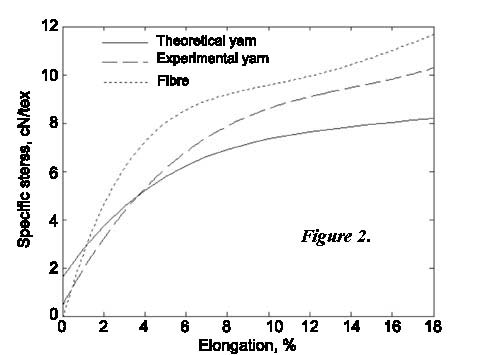
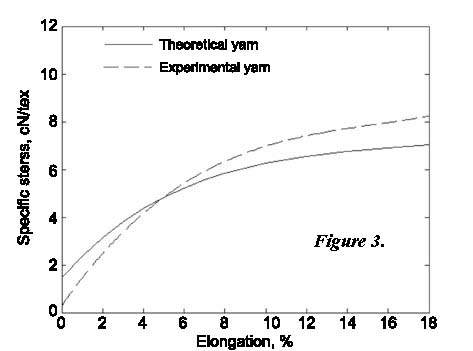
Figure 2.
Figure 3.
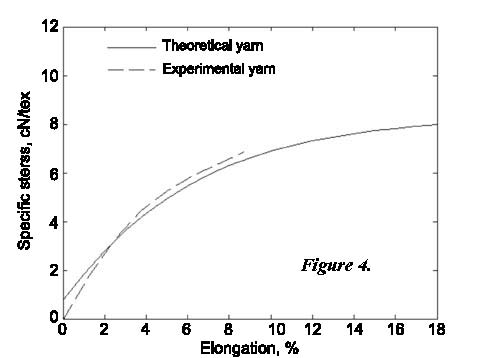
Figure 2. Comparison of theoretical and experimental stress-strain curve of yarn No. 1.
Figure 3. Comparison of theoretical and experimental stress-strain curve of yarn No. 2.
Figure 4.
Figure 4. Comparison of theoretical and experimental stress-strain curve of yarn No. 3.
Appendix
Solution of integral equation (4):
Equations of X and G derived by Hearle [4] are as follows:
Substituting from equation (12) and (13) in equation (4), we then get:
(12)
(13)
(5)
Received 13.09.2005 Reviewed 10.02.2007
